第二届上海大学十大学术进展候选项目简介
(申报编号:XSJZ-202214)

一、学术进展名称及负责人:
气体动力学拟定常可压缩流二维欧拉方程的绕流问题
盛万成(上海大学理学院数学系教授)
二、项目背景:
非线性偏微分方程组理论对数学研究和应用都有着重要意义。自然界中的许多非线性现象如:激波、爆轰波等,都可通过研究非线性偏微分方程组来探索其规律。本成果在气体动力学超音速飞行器的设计研究中用着重要的理论和实际意义。在理论上,高维可压流欧拉方程组的研究一直是流体力学研究充满挑战的课题。在实际应用中,对气体动力学超音速流中,高速飞行器的相关问题,在设计及数值计算等方面都有着关键的作用。气体动力学可压缩流绕尖角的流动是最重要的基本流动之一。它是通过一个中心简单波来实现的。定常流的问题已在Courant 和Friedrichs 的力学名著《Supersonic flow and shock waves》中给出。非定常可压缩流绕尖角向真空扩散的流动之前没有任何结果。本项目研究气体动力学拟定常可压缩流二维欧拉方程的绕凸拐角向真空扩散的绕流问题。
三、学术进展及创新点:
气体动力学拟定常可压缩流绕尖角的超声速流动是最重要的基本流动之一。2018年首次开始研究气体动力学拟定常可压缩流二维欧拉方程的绕凸拐角向真空扩散的绕流问题。与定常流不同的是拟定常流绕凸拐角向真空扩散的绕流问题变成一个中心简单波和平面疏散波的相互作用问题。这是一个全新的课题。构造出二维等熵无旋拟定常流Euler 方程中心简单波,并构造出超声速流绕一凸尖角后形成中心膨胀波或中心压缩波(JHDE,2018),以及等温流的中心膨胀波或中心压缩波(AMM, 2019)。利用特征分解、先验估计和不变区域等方法,得到相互作用区域Goursat问题的整体解,从而构造性地得到了超音速流动绕凸尖角向真空扩散的流动。在不同的情况下,得到了完全疏散波(JMPA, 2018)和不完全部疏散波(ZAMM, 2022) 流动问题的整体解。2021年,我们对于这一问题取得了重大的突破性进展。对拟定常超音速、音速和亚音速来流绕一尖角的向真空扩散绕流问题,由于音速和亚音速来流在尖点处的退化特性,从而具有更大的挑战性。运用尖点附近的双曲扰动方法,结合特征分解、广义特征分析、先验估计和不变区域等方法,通过精细的数学分析,得到该问题整体解的存在性(ARMA,2021)。
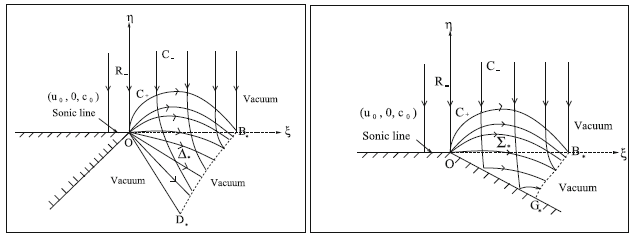
图1气体动力学拟定常可压缩流绕流向真空扩散问题
四、研究成果及应用情况、学术及社会影响:
1. 代表性成果(论著、专利及获奖)
(1) G. Lai and W. C. Sheng, Two-dimensional pseudosteady flows around a sharp corner,Arch. Ration. Mech. Anal., 241(2), 2021, 805–884.
(2) W. C. Sheng and S. K. You, Interaction of a centered simple wave and a planar rarefaction wave of the two-dimensional Euler equations for pseudo-steady compressible flow.J. Math. Pures Appl.,114 (9), 2018, 29–50.
(3) A. D. Yao and W. C. Sheng, Two-dimensional pseudo-steady supersonic flow around a sharp corner.Z. Angew. Math. Mech.,102 (2), 2022, Paper No. e201800270, 16 pp.
(4) W. C. Sheng and S. K. You, The two-dimensional unsteady supersonic flow around a convex corner. J. Hyperbolic Differ. Equ.15 (3), 2018, 443–461.
(5) W. C. Sheng and A. D. Yao, Centered simple waves for the two-dimensional pseudo-steady isothermal flow around a convex corner.Appl. Math. Mech. (English Ed.) 40(5), 2019, 705–718.
2. 学术及社会影响
本成果在气体动力学超音速飞行器的设计研究中具有重要的理论和实际意义。在理论上,高维可压流欧拉方程组的研究一直是流体力学研究充满挑战的课题。2009年“非线性双曲型守恒律方程组的高维黎曼问题”等10个相关课题被列入“10000个科学难题•数学卷"(科学出版社)。相关的Navier-Stokes方程组的问题是美国克莱数学研究所公布的世界千禧年十大数学问题(百万美金)之一。在实际应用中,对超音速流中高速飞行器的设计及数值计算等方面都有着关键的作用。本项目取得的成果发表在应用数学的顶级期刊Arch.Rat.Mech. Anal.(2021年)和J. Math. Pures Appl.(2018年)等上。

